priceskillo.blogg.se

• #CDF FORMULA HOW TO#

#CDF FORMULA HOW TO#

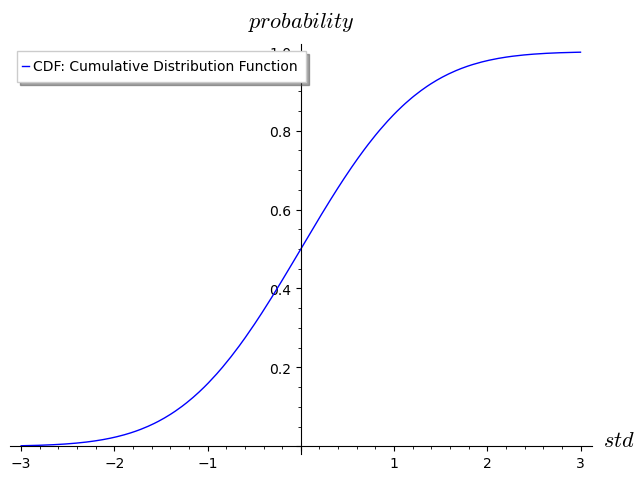
This video will walk through numerous examples of how to find probability using the probability density function and how to create the cumulative distribution function over a sample space. About 68 of values drawn from a normal distribution are within one standard deviation away from the mean about 95 of the values lie within two standard deviations and about 99.7 are within three standard deviations. The properties of a continuous probability density function are as follows. It can be used to get the cumulative distribution function ( cdf - probability that a random sample X will be less than or equal to x) for a given mean ( mu) and standard deviation ( sigma ): from statistics import NormalDist NormalDist (mu0, sigma1).cdf (1.96) 0.9750021048517796. This method can be used for both univariate and bivariate transformations. The cdf technique is especially convenient when the cdf ( )has closed form analytical expression.

Using Property (4), we can write E g 0 ( ln. What is important to note is that discrete random variables use a probability mass function (PMF) but for continuous random variables, we say it is a probability density function (PDF), or just density function. Let ( ) be a function of Y, and our goal is to find the distribution of U. The ramp (or ReLU) transformation of X Y ( X) : X 1 ( X 0) has the CDF F Y ( y) F X ( y) 1 ( y 0) therefore, the expectation of g ( Y) is given by E g 0 ( 1 F X ( y)) d g ( y). The shaded area of the curve represents the probability. This is demonstrated in the graph below for a 0.5. The table utilizes the symmetry of the normal distribution, so what in fact is given is. In contrast, a continuous random variable is a one that can take on any value of a specified domain (i.e., any value in an interval).įor example, the height of students in a class, the amount of ice tea in a glass, the change in temperature throughout a day, and the number of hours a person works in a week all contain a range of values in an interval, thus continuous random variables. This can be used to compute the cumulative distribution function values for the standard normal distribution. What’s the difference between a discrete random variable and a continuous random variable?Ī discrete random variable is a one that can take on a finite or countable infinite sequence of elements as noted by the University of Florida. Let’s jump in to see how this really works! Discrete Vs Continuous Jenn, Founder Calcworkshop ®, 15+ Years Experience (Licensed & Certified Teacher)